In static stress consentration factors are used for brittle material only.
\[\sigma_{max}=k_t \sigma_{nom}\] \[\tau_{max}=k_{ts} \tau_{nom}\]
In Fatigue it is required to use in any cases. However reduced version of k_t is used
\[k_{f}=1+q(k_t-1)\] where q - notch sensitivity
\[\sigma_{max}=k_f \sigma_{nom}\] \[\tau_{max}=k_{f} \tau_{nom}\]
Notch sensitivity is in between 0 and 1. Example for steel is shown below
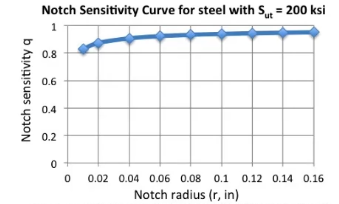
Notch sensitivity could be fount in handbooks (Peterson, Shigley ...) or estimated. For steel
\[q=\frac{1}{1+\frac{\sqrt{a}}{\sqrt{r}}}\]
For steel in bending \[\sqrt{a}= 0.246 - [3.08 \cdot 10^{-3}S_{ult}]+[1.51\cdot 10^{-5}S_{ult}^2]-[2.67\cdot 10^{-8}S_{ult}^3]\]
Fluctuating stress
If no plastic strain at notch stress concentration is used for both midrange and alternating stresses:
\[\sigma_a=k_f\sigma_a\] \[\sigma_am=k_f\sigma_ma\]
If no plastic strain at notch exist stress concentration is used for alternating stress only:
\[\sigma_a=k_f\sigma_a\] \[\sigma_a=\sigma_ma\]