To test material a rotating beam specimen is used
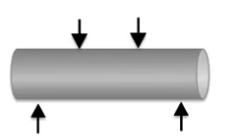
As a result external filament experience fully reversible loading
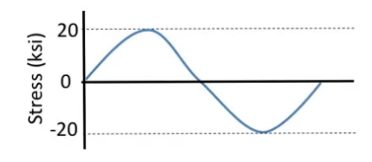
After of series of tests an S-N diargam could be constructed
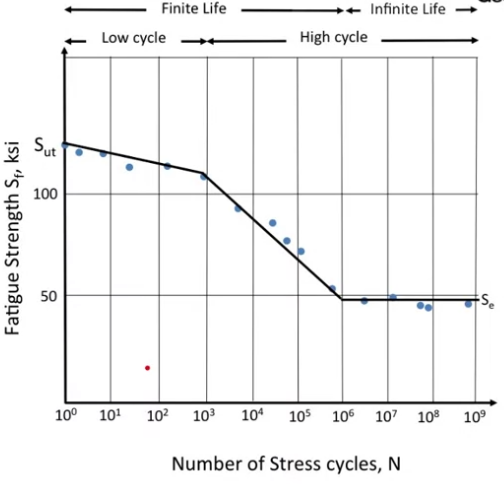
For steel material after 1 000 000 of cycles curve became horizontal. Stress value is called Endurance limit. If repeated stresses are below endurance limit part life is infinite.
Aluminum materials don't have endurance limit. It's just assumed for the analysis
Curve between 10^3 to 10^6 cycles could be approximated with equation: \[S_f=aN^b\] where
\[a=\frac{(fS_{ult})^2}{S_e}\] \[b=-\frac{1}{3}log(\frac{fS_{ult}}{S_e})\] f - fatigue strength fraction of \(S_{ult}\) at \(10^3\) cycles
S_e - endurance limit
Derivative of this equation is \[N=(\frac{\sigma_{rev}}{a})^{1/b}\]
f could be found as: \[f=\frac{\sigma_{F}}{S_{ult}}(2*10^3)^{b}\] where \(\sigma_{F}=S_{ult}+50ksi\) SAE approximation from Fatigue Design Handbook
\(b=\frac{log(\sigma_F/S'_e)}{log(2N_e)}\)
\(N_e\)=endurance limit life
\(S'_e\)=endurance limit of lab specimen
Endurance limit of lab specimen \(S'_e\) could be found in Mil HNDBK 5J. If endurance limit of lab specimen is unknown it could be estimated.
For Steel
\(S'_e=0.5S_{ult}\) - for \(S_{ult}\leq200 ksi (100 MPa)\)
\(S'_e=100 ksi (700 MPa)\) - for \(S_{ult}>200 ksi (100 MPa)\)