Stress concentration factor could not be used for crack tip. Radius \(\rho\) at crack tip is small and concentration factor becomes infinite
\[ K_t = 1+2\sqrt{\frac{a}{\rho}}\]
Griffith solution (1920)
Applied to brittle materials Energy release rate for a wide plate in plane stress with a crack of length 2a
\[ G = \frac{\pi a \sigma^2 }{E}\]
There is a critical energy \(G_c\), defined by tests, exceeding which crack propagates unstable and rapidly
- G < Gc the crack is stable
- G = Gc the crack is in meta-stable equilibrium
- G > Gc the crack is unstable and should propagate
Stress intensity factor
Stress Intensity Factor (K) is the basic parameter in Linear Elstic Fracture Mechanics (LEFM). K is a single parameter which uniquely characterizes the local stress field ahead of a linear elastic crack
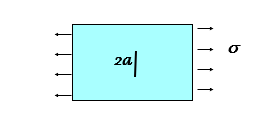
\[ K = \sigma \sqrt{\pi a}\beta\] where
\(\sigma\) - far field stress
\(\beta\) - accounts geometry and crack location
Plasticity effect
1948. G.R Irwin and E. Orowan independently proposed modifications to Griffith's theory to account for plastic energy that is dissipated during the fracture process. This modification made it possible to apply Griffith's theory to metals.
It accounts yielding at crack tip.
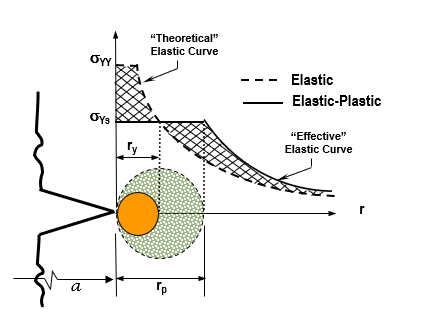
for plain stress (thin plates) \[r_y=\frac{1}{2 \pi}(\frac{K_I}{\sigma-{ys}})\]
for plain strain (thick plates) \[r_y=\frac{1}{2 \pi}(\frac{K_I}{\sigma-{ys}})\]
As a result \[ K = \sigma \sqrt{\pi (a+r_y)}\beta\]
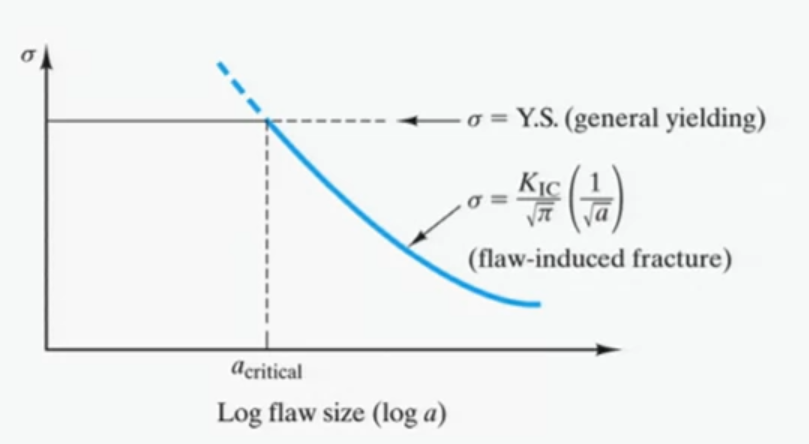
General yielding occurs for flaw sizes less than a critical size, but catastrofic fast fracture occurs above that critical size.
Created: 13 July 2022
Last Update: 31 Aug 2022