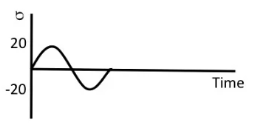
For fully reversed stresses stress amplitude is equal and mean value is equal to zero
S-N curve could be approximated as
\[N=(\frac{\sigma_{rev}}{a})^{1/b}\]
In real life stress patterns are more complex
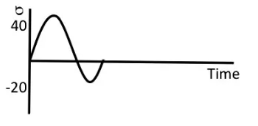
For fluctuating stress Goodman line is used to estimate life
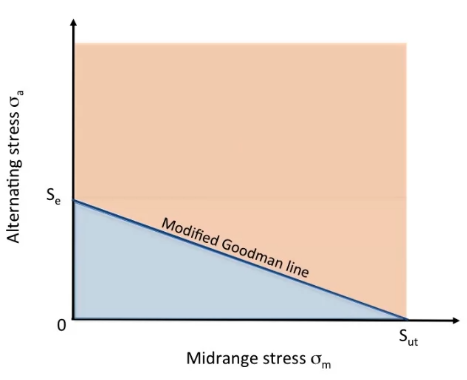
Modified Goodman equation is \[\frac{\sigma_a}{S_e}+\frac{\sigma_m}{S_{ult}}=\frac{1}{n}\]
If n>1 structure has infinite life
Langer criteria (to check if yield exist) is \[\sigma_a+\sigma_m=\frac{s_y}{n}\]
If n<1 structure experience yield
where midrange stress \[\sigma_m=\frac{\sigma_{max}+\sigma_{min}}{2}\]
alternating stress \[\sigma_a=\frac{\sigma_{max}-\sigma_{min}}{2}\]
If component has a finite life, it coulb be estimated using the approach for fully reversible stress. In this case it is required to calculate \(\sigma_{max}\) to have equivalent damage with fluctuating stress. To do so, a line should be constructed from (S_ult, 0) point to ( \(\sigma_{m}\), \(\sigma_{a}\) ) and extend the line to alternating stress axis
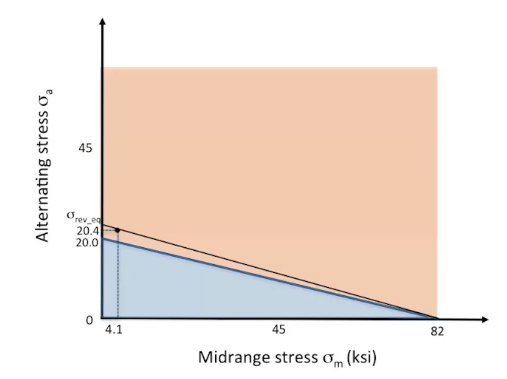
Equivalent stress could be found as: \[\sigma_{rev \_ eq}=\frac{\sigma_{a}}{1-\frac{\sigma_{m}}{S_{ult}}}\]
Life is calculating as: \[N=(\frac{\sigma_{rev \_ eq}}{a})^{1/b}\]
where \[a=\frac{(fS_{ult})^2}{S_e}\]