Under applied Axial load a certain elongation of the bar will take place. The point of load application will move toward the load direction and positive work will be done during this motion.
It is assumed that during the Axial loading all fibers have the same elongation and distribution of force over cross section will be uniform. Axial stress is calculated as a force (F) over area (A): \[\sigma=\frac{F}{A}\]
The elongation of the bar per unit length is calculated as \[\epsilon=\frac{l-l_{init}}{l}=\frac{\delta}{l}\]
In elastic range stresses are proportional to deformations and conform Hook's Law: \[\sigma=E\epsilon\]
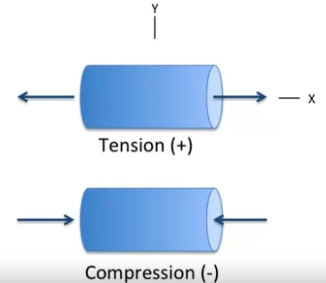
According to sign convention, positive stress means tension and negative - compression.
Rewritten Hook's Law is \[\epsilon=\frac{PL}{AE}\]
Elongation of the bar is proportional to the tensile force and to the length of the bar and inversely proportional to the cross sectional area and to the Modulus of Elasticity.
In case of compression the same equations could be used. Then \(\delta\) will denote total longitudional contraction, \(\epsilon\) - compressive strain, and \(\sigma\) - compressive stress. The Modulus of Elasticity for compression is for the most metals and ceramics the same as for tension.
Created: 06 May 2022
Last Update: 27 Sept 2022